[Algorithm] DP 이해하기

DP(Dynamic Programming)는 완전 탐색, DFS, BFS와 같이 수많은 경우를 따져봐야 할 때

속도가 느려지는 문제를 개선하고자 수행 시간 단축을 목적으로 만들어진 알고리즘이다.

프로그래머스의 정수 삼각형 문제를 예로 들어보자

 

 

 

 

 

 

 

 

 

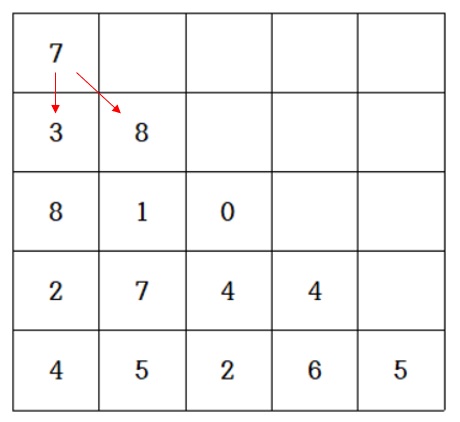
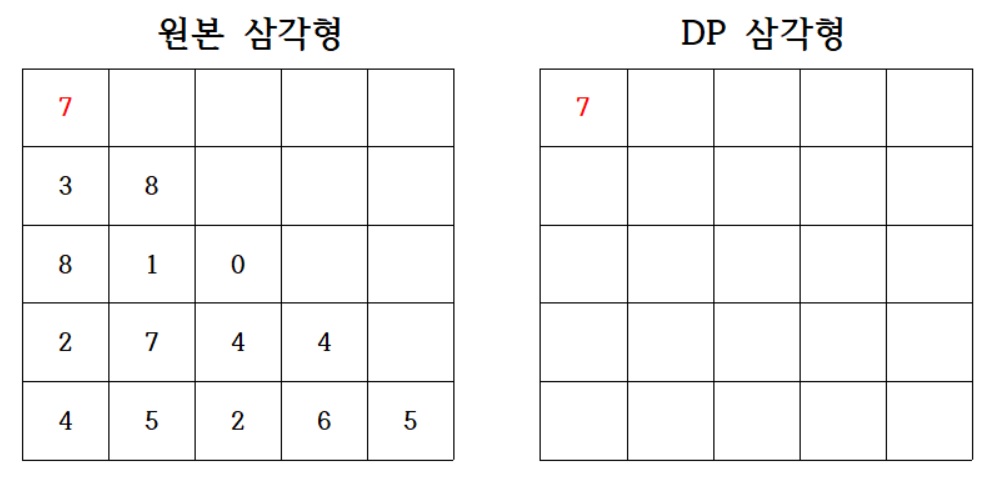
DP 삼각형의 11이 16으로 갱신되었으므로 이제 11을 만들었던 7-3-1 조합은 고려하지 않아도 된다.

 

 

여기서 DP의 장점을 확인할 수 있다.

DP 삼각형을 활용하면 세 번째 줄의 값을 구할 때

두 번째 줄의 값만 확인하고, 첫 번째 줄의 값은 확인하지 않아도 된다.

왜냐하면 두 번째 줄에는 두 번째 줄까지의 모든 조합들 중 최고의 값만 남겨놨기 때문이다.

(이전의 정보를 확인할 필요가 없게 됨)

 

 

다섯 번째 줄까지의 최댓값은 30이며 이 값은 7-3-8-7-5 조합의 결과이다.

 

 

DP의 목적 : 메모리를 사용해서 중복 연산을 줄이고, 중복 연산을 줄여서 수행 속도를 개선한다.

메모리를 사용한다 : 배열 혹은 자료구조를 만든다.

중복 연산을 줄인다 : 연산한 결과를 배열에 담는다.

 

사실 'Dynamic Programming'보다 '기억하며 풀기 알고리즘'이 더 적합한 명칭인 거 같다.

 

DP 문제인지 확인하는 방법

1. DFS / BFS로 풀 수 있지만 경우의 수가 너무 많은 문제

(최대 경우의 수가 500만 개가 넘어간다면 DP로 풀이하는 게 효율적)

2. 경우의 수들에 중복적인 연산이 많은 경우

 

DP 유형의 경우 오래 붙잡고 있기 보다 30분 정도 고민(어떻게 하면 뒤로 돌아가지 않을 수 있을까) 후

답이 안 나오면 풀이를 참고해서 구현만 해보는 방식이 좋다.

현재 단계까지 연산을 잘 했다면 이 연산을 또 하지 않기 위해 어떤 정보를 어떻게 남겨야 할지 생각해 보자